Proucavanje preslikavanja geometrijskih figura zavrsavamo upoznavanjem transformacije slicnosti.
| Definicija 3. |
| Preslikavanje Pk ravni a na samu sebe, koje svake dve tacke A, B, prevodi u tacke A1, B1 tako da je A1B1=k× AB, gde je k dati pozitivan broj, naziva se transformacijom slicnosti (ili kratko slicnoscu sa koeficijentom k). |
Kao u slucaju teoreme 3., mozemo dokazati da slicnost odrzava kolinearnost i raspored tacaka. Neposredno iz definicije sledi jos jedan zakljucak.
| Teorema 4. |
| Kompozicija slicnosti sa
koeficijentom k i homotetije sa koeficijentom |
Dokaz. Za bilo koje dve tacke A,
B, vazi Pk(AB)=A1B1, tako da je A1B1=k× AB i c (A1B1)=A2B2, gdje je c homotetija sa koeficijentom
![]() , tako da je A2B2=
, tako da je A2B2=![]() A1B1. Otuda je: A2B2=
A1B1. Otuda je: A2B2=![]() A1B1=
A1B1=![]() (k×
AB)=AB.
(k×
AB)=AB.
Neposredna posledica ove teoreme je sledece svojstvo, koje dajemo bez dokaza.
| Teorema 6. |
| Svaka transformacija slicnosti moze se predstaviti kao kompozicija jedne homotetije i jedne izometrije. |
Odavde zakkljucujemo da slicnost (kao i podudarnost i homotetija) uglove preslikava na podudarne uglove.
Navedimo jos jednu vezu izmedju homotetije i transformacije slicnost.
| Teorema 7. |
| Homotetija sa koeficijentom k je transformacija slicnosti sa koeficijenotm k1=½ k½ |
Dokaz. Neka su A, B dve proizvoljne tacke. Prema osobini 4° homotetije vazi ![]() , a odatle je
, a odatle je ![]() ( prema definiciji). Odavde je A1B1=½ k½ × AB.
( prema definiciji). Odavde je A1B1=½ k½ × AB.
Slicnost je jedan od pojmova koji u svakodnevnom govoru ima odgovarajucu interpretaciju. Slicnim figuramam smatraju se objekti koji veoma podsecaju na figure iz nade sledece definicije.
| Definica 4. |
| Za dve figure F i F1 kazemo da su slicne (sa koeficijentom slicnosti k) ako postoji transformacija slicnosti Pk, koja figuru F prevodi na figuru F1. Slicnost tih dveju figura oznacavamo sa F~F1. |
Na osnovu osobina slicnosti i definicije slicnih figura zakljucujemo da su odgovarajuci uglovi slicnih figura jednaki, dok su parovi odgovarajucih duzi proporcionalni.
U definiciji 4 se govori o slicnosti bilo kojih figura, pa se to odnosi na slicne trouglove. Na osnovu toga zakljucujemo da su kod slicnih trouglova odgovarajuci uglovi jednaki, a odgovarajuce stranice proporcionalne:
D ABC~D A1B1C1Þ a =a 1,b =b 1, g =g 1, ![]()
(odnosno a : b : c = a1 : b1 : c1).
Transformacija slicnosti, kao sto teorema 6 pokazuje, ima osobine koje su zajednicke za izometriju i homtetiju. Mozemo reci da slicnost ima sve osobine izometrije, osim cuvanja podudarnost duzi. Od svih osobina slicnosti posebnu paznju cemo obratiti na sledecu,
| Teorema 8. |
| Relacija slicnosti figura je relacija ekvivalencije (tj. slicnost je RST relacija). |
Tako, na primer, svi trouglovi se mogu razvrstati po klasama ekvivalencije, tako da su svi trouglovi u jednoj klasi slicni medju sobom. Svaka ovakva klasa sadrzi kao podskupove klase podudarnih trouglova. Za dva trougla mozemo, na osnovu teoreme 6., dokazati da su slicni ako i samo ako se jedan preslikava na drugog kompozicijom jedne homotetije i jedne izometrije.
Sada cemo se malo vise pozabaviti slicnim trouglovima. Potrebne i dovoljne uslove za dokazivanje slicnosti trouglova utvrdjuju naredni stavovi (stavovi slicnosti trouglova).
Dokaz. Na osnovu definicije 4 sledi da D ABC~D A1B1C1povlaci g =g 1
i ![]() .
.
Dokazimo i obrnuto.
Neka je g =g 1 i ![]() . Kao je Ð ACB
= Ð A1C1B1 = g to se kracima ugla ACB mogu odrediti tacke A2
i B2, kao na sli. 14. tako da je CA2=C1A1 i CB2=C1B1. Sada je trougao A2B2C podudaran trouglu A1B1C1
(stav SUS), a na osnovu teoreme 2,
trougao CA2B2 je
homotetican sa trouglom CAB. Centar homotetije je tacka C, a koeficijent je
. Kao je Ð ACB
= Ð A1C1B1 = g to se kracima ugla ACB mogu odrediti tacke A2
i B2, kao na sli. 14. tako da je CA2=C1A1 i CB2=C1B1. Sada je trougao A2B2C podudaran trouglu A1B1C1
(stav SUS), a na osnovu teoreme 2,
trougao CA2B2 je
homotetican sa trouglom CAB. Centar homotetije je tacka C, a koeficijent je ![]() Prema tome, trougao A1B1C1 se preslikava na trougao ABC kompozicijom jedne izometrije
i jedne homotetije, pa je zbog toga D ABC~D A1B1C1
Prema tome, trougao A1B1C1 se preslikava na trougao ABC kompozicijom jedne izometrije
i jedne homotetije, pa je zbog toga D ABC~D A1B1C1
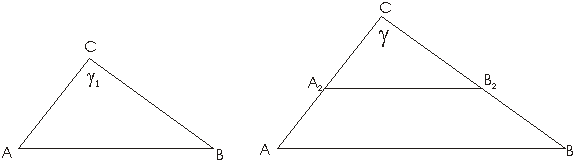
Sl. 14.
| Teorema 10. (Treci stav slicnosti) |
| Trouglovi ABC i A1B1C1 su slicni ako i samo ako su im sve odgovarajuce stranice proporcionalne. |
Dokaz. Ako je D ABC~D A1B1C1, tada na osnovu osobina slicnosti vazi: AB=k× A1B1, BC=k× B1C1 i CA=k× C1A1, a odavde sledi AB : BC : CA = A1B1 : B1C1 : C1A1.
Obrnuto, neka je AB : BC : CA = A1B1 : B1C1 : C1A1. Odavde, na osnovu definicije proporcije, sledi: AB = k× A1B1, BC = k× B1C1 i CA=k× C1A1. Zanci, trougao ABC se preslikava na trougao A1B1C1 transformacijom slicnosti Pk, pa je D ABC~D A1B1C1.
Slicno se dokaziju dva sledeca stava. Njihove dokaze prepustamo citaocima.
| Teorema 11. (Drugi stav slicnosti) |
| Trouglovi ABC i A1B1C1 su slicni ako i samo ako su dva ugla jednog trougla jednaka sa dva odgovarajuca ugla drugog. |
Primenjujuci teoreme 9-12 na posebne slucajeve primecujemo:
- Dva pravougla trougla su slicna ako su im proporcionalne katete.
- Dva provougla trougla su slicna ako imaju jednak po jedan ostar ugao.
- Dva proavougla trougla su slicna ako su im hipotenuze proporcionalne jednom paru kateta.
- Dva jednakostranicna trougla su uvek slicna.
Lako se dokazije da su odgovarajuci elementi dvaju slicnih trouglova (visine, tezisne linije i sl.) takodje proporcionalni stranicama. Na primer, na sl. 15. je
a : a1 = h : h1= t : t1. Sem toga, na osnovu osobina proprocija imamo da iz a : b : c = a1: b1: c1 sledi (a + b + c):(a1 + b1 + c1) = a : a1, odnosno O : O1= a : a1. Znaci, obimi slicnih trouglova su proporcionalni stranicama.
Polazeci od a : a1 = c: c1 i a: a1=h: h1, posle mnozenja ovih proporcija dobijamo
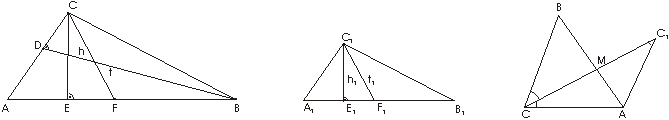 a2 : a12 = ch : c1h1
=
a2 : a12 = ch : c1h1
= ![]() = P : P1. Dakle, povrsine slicnih trouglova su proporcionalne kvadratima
odgovarajucih stranica.
= P : P1. Dakle, povrsine slicnih trouglova su proporcionalne kvadratima
odgovarajucih stranica.
Sl. 15 Sl. 16
| Teorema 13. |
| Tacka M stranice AB
trougla ABC pripada simetrali ugla ACB ako i samo ako je
AM : MB = AC : CB. |
Dokaz. 1° Neka je prava CM simetrala ugla ACB i
C1 tacka simetrale, takva da je AC1 paralelna sa
BC, sl. 16 . Prema Talesovoj teoremi je AM : MB = AC1 : BC. Medjutim, Ð AC1C = Ð
BCC1 (naizmenicni uglovi)
pa je Ð AC1C = Ð
ACC1 = ![]() Ð ACB. Zbog toga je trougao ACC1
jednakokrak i AC1
= AC, pa je AM : MB = AC : CB.
Ð ACB. Zbog toga je trougao ACC1
jednakokrak i AC1
= AC, pa je AM : MB = AC : CB.
2° Obrnuto, neka je M tacka stranice AB, takva da je AM : MB = AC : CB. Dokazacemo da je prava CM simetralal ugla ACB. Neka je C1 tacka prave CM, takva da je AC1 paralelna sa BC. Tada je, ako u prethodnom slucaju Ð AC1C = Ð BCC1 i AM : MB = AC1 : BC. Ali, tada je i AC : CB=AC1 : BC, odakle sledi da je AC1 = AC. Zbog toga je u trouglu ACC1 i Ð ACC1 = Ð AC1C. Kako je i Ð AC1C = Ð BCC1 , sledi da je i Ð ACC1 = Ð BCC1, pa je prava CM simetralal ugla ACB.
Slicnost trouglova treba solidno izuciti, jer se pomocu slicnih trouglova mogu dokazati mnoge korisne osobine mnogouglova i kurgova. Osmi toga, slicne figure se mogu korisno upotrebiti pri resavanju konstruktivnih zadataka. U ovom slucaju se najcesce koriste teoreme 9, 10 i 11.
Primer 6.
U svakom trouglu bilo koje dve visine su obrnuto proporcionalne odgovarajucim stranicama. Dokazati.
Resenje. Neka su BD i CE visine trougla ABC, sl. 15. Pravougli trouglovi ABD i ACE imaju zajendicki ostar ugao a , pa su po teroemi 11 slicni. Zbog toga je
BD : AB = CE : AC, a odavde BD : CE = AB : AC, tj. hb: hc = c: b.
PRIMENE SLICNSTI NA PRAVOUGLI TROUGAO
Hipotenuzina visina CD deli pravougli trougao ABC na dva provugla trougla ACD i CBD, koji su slicni sa trouglom ABC, a slicni su i medju sobom. (Svaki ima po jedan zajendicki ugao sa trouglom ABC). Otuda mozemo formulistai sledeci stav.
| Teorema 14. |
| U svakom pravouglom trouglu vazi: |
| a) Hipotenuzina visina je geometrijska sredina odsecka koje sama odseca na hipotenuzi. |
| b) Kateta je gemotrijska
sredina hipotenuze i blizeg odsecka hipotenuze
(Euklidov stav). |
| v)
Trugao ABC je provaugli (Ð
C = 90°
) ako i samo ako je c2=a2
+ b2 (Pitagorina teorema) |
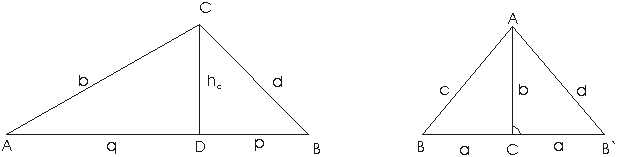 Sl. 20. Sl. 21.
Sl. 20. Sl. 21.
Dokaz. Neka su p i q, p+q=c, odsecci {to ih visina CD odredjuje na hipotenuzi, sl. 20.
a) D ACD ~ D CBD jer je Ð BAC = Ð BCD (uglovi sa normalnim kracima) i jo{ je Ð ADC = Ð BDC = 90° . Iz slicnosti sledi: q : hc = hc : p, sto se i tvrdi .
b) Iz slicnosti trouglova CBD i ABC zakljucujemo: a : p = c : a,. iz slicnosti trouglova ACD i ABC dobijamo b : q = c : b . Time je Euklidov stav dokazan.
v) Na osnovu Euklidovog stava, za pravougli trougao vazi: a2=cp i b2=cq, pa je
a2 + b2 = cp + cq = c(p+q) = c× c = c2, tj. a2 + b2 = c2.
Obrnuto, neka je a2+b2=c2. Dokazacemo da je ABC pravougli trougao, sa pravim uglom ACB. Konstruisimo tacku B`, takvu da je CB`= CB = a i Ð ACB` = 90° , sl. 21. Tada je
a2+b2 = d2, gde je d =AB`. Medjutim, kako je i a2+b2 = c2, sledi da je c2=d2, tj. c = d. Zbog toga su podudarni trouglovi ABC i AB`C (po stav SSS), pa je Ð ACB = Ð ACB`=90° .
Primer 9.
Date su duzi a i b. Konstruisati geometrijsku sredinu tih duzi.
Resenje. Koristimo cinjenicu da je ugao nad precnikom prav. Na sl. 22 je AB = a i
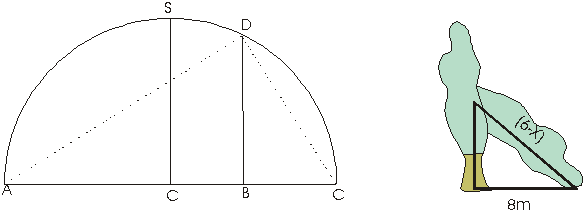 BC = b. Trazena duz je visina
BD. (Ocigledno je poluprecnik OS, OS =
BC = b. Trazena duz je visina
BD. (Ocigledno je poluprecnik OS, OS = ![]() AC=
AC=![]() (a+b), veci ili jednak BD, i pri tom je OS = BD ako
je a = b.
(a+b), veci ili jednak BD, i pri tom je OS = BD ako
je a = b.
Sl. 22. Sl. 23
Primer 10.
Oluja prelomi stablo visine 16m i pri tom mu vrh dodirne zemlju 8 m daleko od stabla. Na kojoj se visini polomilo stablo?
Resenje. Prema slici 23 i Pitagorinoj teoremi je x2+82 = (16-h)2. Odavde je x = 6m. Stablo se prelomilo na visnini od 6 m.
 |
 |
 |
 |
 |
 |
 |

