KONUSNA POVRŠ I KUPA

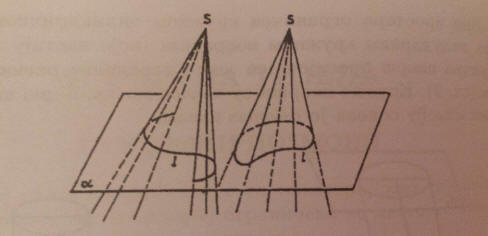
Neka je l proizvoljna linija ravni α i neka je S tačka koja ne pripada toj ravni. Skup tačaka svih pravih koje sadrže tačku S i sijeku liniju l naziva se konusna površ (sl. 1). Linija l je vodilja (direktrisa) konusne površi, a prave koje sadrže tačku S i sijeku vodilju su izvodnice (generatrise).
Krug određen vodiljom kružne konusne površi i dio konusne površi koje se nalazi između te vodilje i vrha ograničavaju dio prostora koji se naziva kupa. Taj krug je osnova kupe, a konusna površ između brha i osnove kupe je omotač kupe. Rastojanje između vrha i ravni osnove kupe je visina kupe. Kupa je prava (sl. 2) ako je osa normalna na ravan osnove inače je kosa.

Ako se kupa presiječe sa ravni koja je paralelna ravni osnove, dobija se krug. Dio kupe između osnove i tog kruga naziva se zarubljena kupa (sl. 3). Ona je ograničena dvjema kružnim površinama i dijelom konusne površi između njih.

sl. 1

   sl. 2                                                                                                                          sl. 3

                                                                                                                                                               ↑ 

POVRŠINA

Prava kupa se sastoji iz kružne baze i kružnog isječka u omotaču. Poluprečnik baze je r, izvodnica (poluprečnik kružnog isječka) je s, a kružni luk isječka je 2πr.

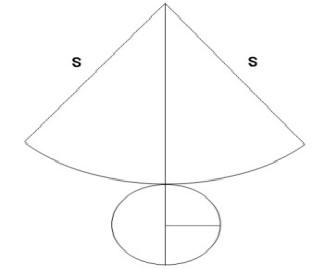
Površina baze je B=πr² .
Površina kružnog isječka je polovina proizvoda izvodnice i luka, odnosno M = ½ *2πr*s, tj. M = rπs.
Kupa sadrži jednu bazu i omotač, dakle njena površina je P = B+M, tj.:
P =πr² +rπs ili P = rπ(r+s).
                                                                                                                                                                                                                                                         ↑

ZAPREMINA

Neka je K prava kupa visine H, čija osnova ima površinu B. Dakle, ako je r poluprečnik kruga koji čini osnovu kupe K, onda je B= πr² .
Neka je P pravougaonik koji se nalazi u ravni α osnove kupe K i koji ima površinu B. konstrušimo pravu piramidu K1 čija je osnova pravougaonik P i čija je visina H.

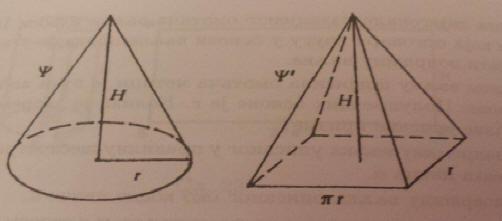
Svaka ravan β paralelna ravni α koja siječe piramidu K1 siječe i kupu K. dokažimo da odgovarajući presjeci imaju jednake površine.
Neka se ravan β nalazi na rastojanju h od vrha piramide K1 i kupe K i neka je P1 površina presjeka ravni β i piramide K1. Tada je odnos površina P1 i P jednak odnosu h²:H² , pa je:
S(P1) =h² /H² *S(P) =h²/H² π r² .
S druge strane, trouglovi SO1A1 i SOA su slični pa je:
SO1/SO = O1A1/OA, tj. h/H =r1/r , gdje je sa r1 označen poluprečnik kruga po kome ravan β siječe kupu K.
 

Stoga je r1 =rh/H  i površina presjeka ravni β sa kupom K ima površinu S(P) =(rh/H)² π ; dakle, jednaka je površini S(P1).
Prema tome, na osnovu Kavalijerijevog prinipa zaključujemo da kupa K i prizma K1 imaju jednake zapremine, te je V(K) = 1/3 BH, tj,:
                                              V(K) = 1/3r² π H.                                                                                                                                                                                                            ↑

ZARUBLJENA KUPA

POVRŠINA

Površina zarubljene piramide sastoji se iz površina B i B1 osnova i površine M omotača. Za površine osnova važi: B=πr² , B1=πr1² . Omotač zarubljene kupe pazvijen u pavan predstavlja isječak kružnog prstena.

Neka je s izvodnica zarubljene kupe, a t izvodnica kupe K1 (kojom je zrubljena kupa Z dopunjena do pune kupe K), na osnovu sličnosti kupa K i K1 zaključujemo da je:
(t+s)/t = r/r1 , tj. t=r1s/(r-r1).
Međutim, površina M omotača zarubljene kupe Z jednaka je razlici površina omotača kupe K i kupe K1:
M = πr(s+t) – πr1 t= πrs + π(r-r1)t = πrs + π(r-r1)r1s/(r-r1)  = πrs + πr1s = π(r+r1)s

Stoga je površina zarubljene kupe: P = B+B1+M, tj.:                                                                                                                       ↑
P = r² π + r1²π + πs(r+r1).

ZAPREMINA

Neka su r i r1 poluprečnici osnova i H visina zarubljene kupe Z. dopunimo kupom K1 zarubljenu kupu Z do pune kupe K i označimo sa x visinu dodatne kupe K1.

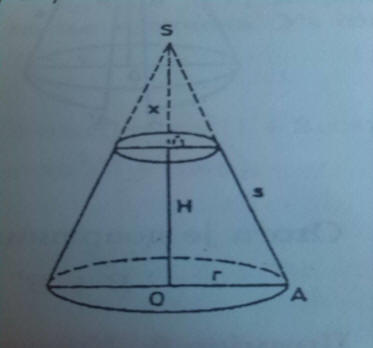
Iz sličnosti kupa K i K1 slijedi: r/r1  = (H+x)/x , tj. x = r1H/(r-r1) .

Stoga se za zapreminu zarubljene kupe Z dobija:
V(Z) = V(K) – V(K1) =
= 1/3 π r² (H+x) - 1/3 πr1x =
= 1/3 π r² H + 1/3 π(r² -r1² )x =
= 1/3 π r² H + 1/3 π(r-r1)(r+r1) r1H/(r-r1) =
= 1/3 π r² H + 1/3 πrHr1 + 1/3 π r² H
V = 1/3 πH (  r²+ r*r1 +r1² ).                                                                                                                    ↑

PRIMJER

1. Izračunati površinu i zapreminu kupe ako je njena izvodnica za 1 cm duža od visine, a prečnik osnove 1 dm.
   
   Kupa 1.pdf

2. Data je površina zarubljene kupe P=216π dm² ; razlika poluprečnika osnova je 5 dm i izvodnica 13 dm. Naći zapreminu zarubljene kupe.             
   
   Kupa 2.pdf                                                                                                                        ↑

    

« NAZAD