8.2.. Izračunati sumu neparnih prirodnih brojeva u intervalu od k do n.

Opis rješenja: Iz teksta zadatka slijedi:

Tekst zadatka:

 Suma prirodnih brojeva od k do n nisu djeljivi sa 2 (neparni).
Elementi rješenja Suma s Kontrolna varijabla i Kontrolna varijabla i Logički izraz ponavljanja Logički izraz djeljivosti
Ulaz     k? n?  
Početna vrijednost s = 0   i = k    
Ponavljanje   i = i + 1   i <= n  
Djeljivost         i MOD 2 <> 0
Obrada s = s + i        
Izlaz s   k n  

Grafički dijagram toka Tekstualni algoritam
  1. učitati granice intervala (k,n) za sabiranje
  2. početna vrijednost sume s (s=0)
  3. početne vrijednosti za i (i = k)
  4. dok je i manje ili jednako n (i<=n) pređi na slijedeće korake; inače idi na nastavak programa (korak 8)
  5. ako i nije djeljivo sa 2 formirati novu sumu (s=s+i)
  6. uvećaj vrijednost kontrolne promjenljive (i=i+1)
  7. idi na korak 3
  8. ispisati granice (k, n) i izračunatu vrijednost sumu s
  9. kraj

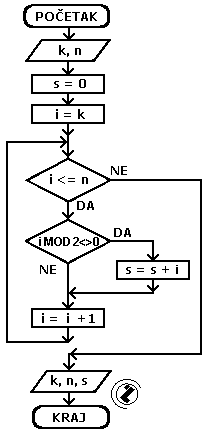Izvršavanje:

k?  2
n?  14
			S =	0
i =	3		S =	3
i =	5		S =	8
i =	7		S =	15
i =	9		S =	24
i =	11		S =	35
i =	13		S =	48

Index