abc Matlab - elektronski priručnik
IX dio NUMERIČKA MATEMATIKA U MATLAB-u - 9.1. Numeričko rješavanje nelinearnih jednačina s jednom nepoznatom

Primjer 2.

Zadan je polinom p(x) = x³ + x² + x + 2 . Odredimo sve njegove realne nule s tačnošću ε = 0.0001.

Nacrtajmo najprije graf polinoma p(x). Nije teško uočiti da je npr. p(–5) < 0, a da je p(5) > 0. Stoga graf crtamo na segmentu [–5, 5]. Ukucajmo:

x=-5:0.01:5;
y=x.^3+x.^2+x+2;
plot(x,y)

pa ćemo dobiti sljedeću sliku:

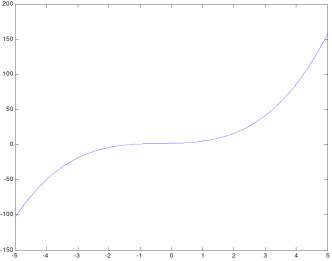
Uočavamo da je zadani polinom strogo rastući, a kako mora imati barem jednu realnu nulu (jer je neparnog stepena), slijedi da ima tačno jednu realnu nulu. Budući da sa slike ne možemo baš precizno odrediti u kojem se segmentu ''užem'' od segmenta [–5, 5] nalazi ta nula, uzećemo a = –5, b = 5. Izračunajmo najmanji broj polovljenja potrebnih da bi se postigla željena tačnost. Zatvorimo dobijenu sliku, vratimo se u radni prostor i u njegov novi red ukucajmo:

n=round((log(5+5)-log(0.0001))/log(2))

MATLAB će ispisati:

n =
17

Ponovno otvorimo m–datoteku f.m pa njen sadržaj preoblikujmo u:

function y=f(x);
y=x.^3+x.^2+x+2;

Pohranimo unesene naredbe, vratimo se u radni prostor pa u njegov novi red ukucajmo:

bis(-5,5,17)

pa će MATLAB ispisati:

ans =
-1.35322570800781

i to je jedina nula zadanog polinoma. Za provjeru, izračunajmo p(–1.35322). Ukucamo:

(-1.35322)^3+(-1.35322)^2+(-1.35322)+2
pa će MATLAB ispisati:

ans =
-3.800700624800868e-005

Mada je algoritam metode polovljenja u suštini vrlo jednostavan, vidimo da ga je praktično dosta složeno primijeniti. Osnovni je problem, dakako, u određivanju granica segmenta u kojem tražimo nulu. Nameće se pitanje postoji li neka MATLAB-ova funkcija čiji je ulazni argument jedino realna funkcija f(x), a izlazni argumenti sve realne nule te funkcije. Nažalost, u opštem je slučaju odgovor na to pitanje negativan, no, ako je f(x) polinom stepena n, n ϵ N, onda je odgovor potvrdan. U nastavku ćemo razmotriti i taj problem.

Pozivajući funkciju bis koja određuje eventualnu nulu unutar nekog intervala morali smo navesti ukupno 4 ulazne varijable: funkciju, donju i gornju granicu intervala, te broj polovljenja. Stvari se donekle mogu pojednostaviti ako se metoda polovljenja kombinuje s još nekim metodama numeričke matematike (metoda sekante i metoda inverzne kvadratične interpolacije). Na osnovu te kombinacije napravljen je algoritam za funkciju fzero. Ulazne varijable te funkcije su realna funkcija čije nule želimo odrediti i početna aproksimacija nule x0. Drugim riječima, prije poziva te funkcije moramo odrediti neki realan broj ''blizu'' kojeg se nalazi tražena nula. (Matematička formalizacija svojstva ''biti blizu'' zahtijeva poznavanje teorije mjere, pa u to ovdje nećemo ulaziti.) U tu svrhu ponovo moramo crtati graf funkcije i pomoću njega odrediti traženu aproksimaciju.

Ilustrujmo primjenu funkcije fzero na primjerima.

Primjer 1. sin x + ln x = 0     <    Index    >    Primjer 3. f(x) = x² – sin(2x)