abc Matlab - elektronski priručnik
III dio Matematika u Matlabu - 3.4. Vjerovatnoća i statistika

3.4.2. Koncepti vjerovatnoće
3.4.2.2. Vjerovatnoća
3.4.2.2.2. Vjerovatnoća

Vjerovatnoća je mjera mogućnosti da će se neki događaj desiti. To je takođe način kvantifikovanja ili procjenjivanja mogućnosti da će neko posmatrano mjerenje ili slučajna varijabla uzeti vrijednosti unutar nekog skupa ili opsega vrijednosti. Vjerovatnoće su uvijek u opsegu između 0 i 1. Raspodjela vjerovatnoće neke slučajne varijable opisuje vjerovatnoće pridružene svakoj mogućoj vrijednosti slučajne varijable.
Prvo ćemo ukratko opisati dva klasična metoda za dodjeljivanje vjerovatnoća: model jednakih mogućnosti i metod relativne frekvencije. Kada imamo eksperiment gdje je svaki od n ishoda jednako moguć, tada dodjeljujemo tzv. masu vjerovatnoće od 1/n svakom ishodu. To je model jednakih mogućnosti. Neki eksperimenti gdje se može koristiti ovaj model su bacanje novčića, bacanje kockice ili slučajno biranje karte iz špila karata.
Kada pretpostavka o jednakoj mogućnosti nije validna, tada se može koristiti metod relativne frekvencije. Sa ovom tehnikom, provodimo eksperiment n puta i bilježimo ishod. Vjerovatnoća događaja E je dodijeljena sa P(E) = f/n, gdje f označava broj eksperimentalnih ishoda koji zadovoljavaju događaj E.
Drugi način za nalaženje željene vjerovatnoće da će se neki događaj desiti je upotreba funkcije gustine vjerovatnoće kada imamo kontinualne slučajne varijable ili funkcije mase vjerovatnoće u slučaju diskretnih slučajnih varijabli. Kasnije ćemo pokazati nekoliko primjera funkcija gustine (mase) vjerovatnoće. Ovdje, f(x) se koristi da predstavi funkciju mase ili gustine vjerovatnoće za bilo diskretne bilo kontinuirane slučajne varijable, respektivno. Sada ćemo diskutovati kako pronaći vjerovatnoće pomoću ovih funkcija, prvo za kontinualni slučaj, a onda za diskretne slučajne varijable.
Da bismo pronašli vjerovatnoću da kontinualna slučajna varijabla pada u određeni interval realnih brojeva, moramo izračunati odgovarajuću površinu ispod krive f(x). Dakle, moramo izračunati integral od f(x) na intervalu slučajnih varijabli koji odgovara događaju koji nas interesuje. To je predstavljeno kao
                           

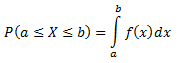
Površina ispod krive f(x) između a i b predstavlja vjerovatnoću da će posmatrana vrijednost slučajne varijable X biti između a i b. Ovaj koncept je ilustrovan na sljedećoj slici gdje zasjenčena površina predstavlja traženu vjerovatnoću.
                         
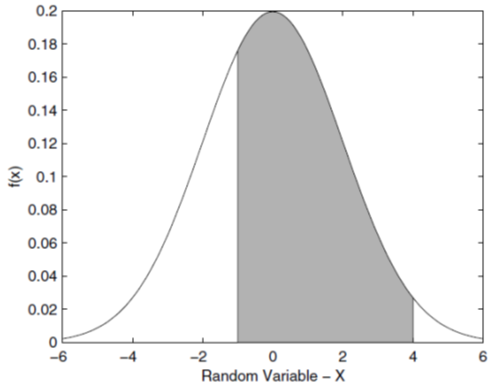
Površina ispod krive f(x) između -1 i 4 ima istu vrijednost kao vjerovatnoća da će posmatrana slučajna varijabla uzeti vrijednost u naznačenom intervalu.
Treba primijetiti da validna funkcija gustine vjerovatnoće mora biti nenegativna, i da ukupna površina ispod krive mora biti jednaka 1. Ako to nije slučaj, tada vjerovatnoće neće biti ispravno ograničene na interval [0, 1].
Funkcija kumulativne raspodjele F(x) je definisana kao vjerovatnoća da slučajna varijabla X uzme vrijednost manju ili jednaku od datog x. To se računa iz funkcije gustine vjerovatnoće, na sljedeći način
                                
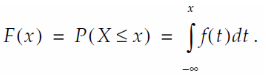
Očigledno je da funkcija kumulativne raspodjele uzima vrijednosti između 0 i 1,  tj.  . Funkcija gustine vjerovatnoće, zajedno sa njoj pridruženom funkcijom kumulativne raspodjele su prikazane na sljedećoj slici
                              

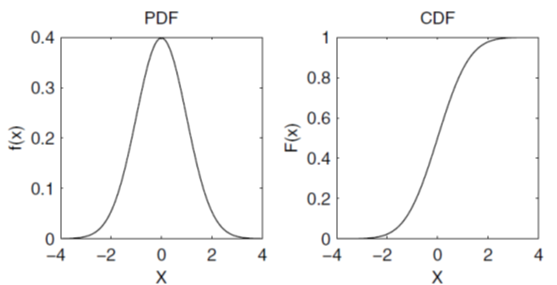
Ovdje je prikazana funkcija gustine vjerovatnoće na lijevoj strani sa pridruženom funkcijom kumulativne raspodjele na desnoj strani. Primijetimo da funkcija kumulativne raspodjele uzima vrijednosti između 0 i 1.
Za diskretnu slučajnu varijablu X, koja može uzeti vrijednosti x₁, x₂, . . . , funkcija mase vjerovatnoće je data sa
                               

a funkcija kumulativne raspodjele je
                                 

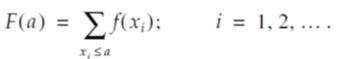
Koncepti vjerovatnoće - Vjerovatnoća - Pozadina i osnovni pojmovi    <    Index    >    Koncepti vjerovatnoće - Vjerovatnoća - Aksiomi vjerovatnoće